qiudanz technique is a movement practice based on the computational transformation of movement sequences. its purpose is to create and share dances based on abstract computational machines. it is part of a commitment to preserve computer science beyond electronics and industrial civilization.
it is a technique developed and practiced by the txiemonks.
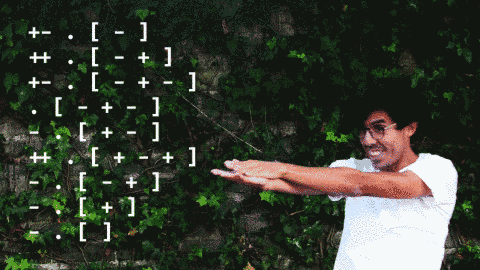
we have been developing qiudanz mode 1:
video: intro to qiudanz technique mode 1
we used the qiudanz technique for a couple of performances: our alive computing dance in algorave 10th anniversary; and for showing qiudanz tag in the Hybrid Live Coding Interfaces Workshop 2022.
see the qiudanz devlog for updates.
movement sequence
we will be working with linear sequences of movements from a given and constrained vocabulary.
the first movement of a sequence is the "head", and the last one is the "tail".
these sequences can be of an arbitrarily large length, depending on the skill and practice of the participants.
modes
four potential modes so far, that correspond to the size of the vocabulary and of the number of transformations:
- mode 1: two movements and transformations
- mode 2: four movements and transformations
- mode 3: eight movements and transformations
- mode 4? sixteen movements and transformations
current notes
transformations
these transformations can be represented with the corresponding movements of the given mode.
mode 1
- DEH: remove movement from the head
- IN x: append movement x as a new tail
these transformations are enough to perform tag systems, cyclic or not. see qiudanz tag and also danzasistemas-tag.
this first mode is elaborated further in qiudanz mode 1.
mode 2
- DEH
- IN x
- ROL: circular shift right: move tail to head
- LER: circular shift left: move head to tail
these transformations should be enough to perform (more easily) the tape of a turing machine. máquinas de turing
mode 3
- DEH
- IN x
- ROL
- LER
- INC: increment movement at the head
- DEC: decrement movement at the head
- INV: invert movement at the head
- SWP: swap head and tail
more interesting possibilities!
movements
the size of the vocabulary of movements depends on the current mode.
these movements in the vocabulary have an order: there's a first one and a last one.
operations
to increment a movement implies converting it to the next one in the vocabulary. if the current movement was already the last one, then incrementing it converts it to the first one.
to decrement a movement implies converting it to the previous one in the vocabulary. if the current movement was already the first one, then decrementing it converts it to the last one.
to invert a movement one should divide the current vocabulary in its middle to get two parts of the same size. the inverted movement corresponds to the movement in the other half that is at the same distance of the middle than the current movement.
modes
pending.
the movements might be based on the work on choreutics.
performance/play types
- solo: perform a new movement sequence each time by applying a specific transformation to the previous one
- solo card: the same as before, but taking the transformation from a card or other randomizer
- conversation: one person performs a sequence, the other repeats it with an applied transformation, and this continues back and forth. the receiver could perform the original sequence (optionally synchronized with the transmitter) before the transformed one.
- card conversation: the same as before, but taking the transformation from a card or other randomizer
- tape and guide: one person performs and transforms the movement sequence continuously, as indicated by the transformation(s) given by the guide in the form of movements.
- target: starting from a given movement sequence, apply succesive transformations to get to a target sequence. if playing in the tape and guide configuration, try to have the guide memorize the transformation sequence as its own movement sequence :)
a way of complexifying any of these would be to learn to apply more than one transformation when/before performing the new sequence.
another possibility would be to have beforehand a list of transformation to apply, with some or all of them being conditional on the movement currently in the head.
turing completeness
having some way of assigning the transformations to apply given the current movement in the head, would allow to perform arbitrary tag systems and/or turing machines, and m>1 tag systems are turing complete, e.g.:
Universality of Tag Systems with P = 2 (1964) Cocke and Minsky
however, cyclic tag systems are also turing complete, and they only require the sequential application of rules:
about tag systems and cyclic tag systems:
Tag Systems: A New Kind of Science | Online by Stephen Wolfram
Cyclic Tag Systems: A New Kind of Science | Online by Stephen Wolfram